Soft Actor Critic을 처음 발표한 논문은,
DQN 논문처럼 "와! 직관적이다!" 하는 감탄을 자아내지는 않는다.
기본적으로 '엔트로피'라는 추상적이기 그지없는 개념을 사용하는 것으로
학습의 목적함수를 설정하고 나섰기 때문이기도 하다.

SAC의 목적함수는 위와 같이, 총 에피소드에서의 보상과 함께
엔트로피의 합을 최대화하는 것이다.
일반적으로 엔트로피가 큰 상태는, 굉장히 어질러져 있는 것을 의미하므로
목적함수는 이렇게 말하는 것이다.
"보상을 최대화시키는 행동지침을 짜 와! 그런데 학습이 충분히 랜덤화되어 있어야 해!"

이를테면, "집안 곳곳을 잘 둘러보되
기름이 담긴 찻 숟가락도 온전히 보전해오게"라고 하는 옛 현자의 말(꼬장)과 비슷하다.
다행인 것은, 집안을 둘러보면서 조심조심 찻 숟가락을 들고 있는 것은
온전히 컴퓨터(SAC 학습 시스템)의 몫이고,
우리는 그저 집 구조를 짜놓고 명령만 내리면 된다는 것이다.
옛 현자가 본다면 이마를 탁! 치는 광경이 아닐 수가 없다.
논문에서는 이 목적함수(엔트로피가 포함되어 있다)를 극대화 하는 과정을
1) Policy Iteration 알고리즘을 도입해서 먼저 설명한 뒤에
2) Actor-Critic 알고리즘과 병합해서
Soft Actor Critic을 완성한다.
Maximum Entropy - Policy Iteration의 경우
Policy Iteration는, CS234 강의 중에서도 2강에 나왔을 정도로 기본적인 알고리즘이다.
Policy Q Value의 평가 -> 행동지침 개선으로 이뤄지며
상당히 직관적이지만, 모델이 명백하게 주어진 상황에서만 적용가능하다.
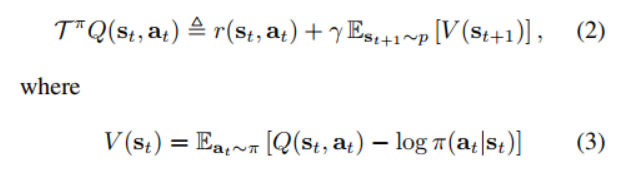
Q Value의 평가(Policy Evaluation)는 위 식을 반복하면서 이뤄지는데,
언뜻 보더라도, DDPG 알고리즘을 설명하면서 봤던
Target Update(Q가 중복되어 등장하는 것)가 포함되어 있는 것을 확인할 수 있다.

행동지침 개선(Policy Improvement)은 위 식을 따라서 이뤄진다.
D_KL이니, exponential 함수니, Z 분포니 하는 것들이 죄다 등장하면서
뒤통수를 맞는 느낌이 들긴 하지만,
꼼꼼히 따져보면 그렇게 새로운 내용은 아니다.
우선 3번 식에서 Q - log $\pi$ 에 exp()를 씌워주게 되면
exp(Q - log$\pi$)가 되는데, 이 식이 바로 4번 식에서 괄호의 우변에 있는 내용이다.
같은 내용에 로그를 씌웠다가 벗기는 이유는,
현실 세계의 확률이 로그 안에서는 보다 정규분포에 가까워지는 현상이 있기 때문이기도 한데,
정확한 이유는 현재로서는 넘어가도록 하겠다.
어쨌든 결국 4번 식이 의미하는 것은,
기존의 행동지침과 크게 다르지 않은 범위에서 새로운 행동지침을 찾아내겠다는 것을 의미한다.
"엥? 그냥 기존 행동지침이랑 비슷하게만 만들어주면 더 개선이 된다구?"
하고 혼란스러워 하는 사람들을 위해, 논문에서는 친절하게 부록을 할애하여 증명을 해줬다.
강의를 들을 때는 "이런 증명 방법이 있다더라!" 하면서 넘어갔지만,
논문까지 읽어보는 입장에서도 그러고 넘어갈 수가 없어서 꾸역꾸역 읽어보았다.
증명은 아래와 같이 총 네 단계로 이뤄진다.
1.

J는 단순히 위 항을 간추린 것에 불과하므로, 목적함수 J와 헷갈리지 말자.
여튼 새로운 행동지침은 위와 같이 정리될 수 있다.
2.

16번 식을 만족하는 행동지침을 위 부등식도 만족하게 된다.
어쨌거나 J를 최소화 하는 행동지침을 골랐기 때문이다.
3.

그러므로 17번과 같은 부등식도 도출해낼 수가 있다.
이는 새로운(new) $\pi$와 exp(Q) - log(Z) 간의 차이가
기존(old) $\pi$와 exp(Q) - log(Z)보다 덜 나기 때문이다.
그런데 log (Z) 부분은 상수이므로 소거해줘도 별 지장이 없다.
4.

남은 부분을 잘 살펴보면, (3) 식과 같이 Value function과 동일하다는 것을 알 수 있다.
ㄴㅇㄱ
결국 새로운 행동지침으로 계산한 V, 곧 Q 값이 더 우수하다는 것이다.
이렇게 Policy Iteration에 Maximum Entropy 를 적용할 경우를 살펴보았다.
하지만 말했듯, 모델이 주어지는 경우에만 적용가능한 알고리즘이므로
Actor Critic에 적용하는 경우를 확인해야 한다.
Maximum Entropy - Actor Critic의 경우
모델이 주어지지 않는 경우에는 V, Q, $\pi$를 모두 근사치로 변환해줘야 한다.
큰 틀은 Policy Iteration과 동일한 채로,
참값이 주어졌던 변수들을 죄다 업데이트 시켜줘야 한다는 점만 다르다.

결과

초록색과 주황색 그래프만 보면 된다.
그렇게 깔끔하게 코딩이 되었던 DDPG(초록색)는
조금만 환경이 복잡해지자 고전을 면치 못한다.
반면 주황색(SAC)은, 알고리즘은 복잡하기 짝이 없지만
성능은 기깔나게 잘 나온다.
다음 편에서는 실제 코드에서 SAC를 어떻게 구현했는지 살펴봐야겠다.
추가 관련 글
1) Soft-Actor Critic을 활용한 정책만들기
강화학습(SAC)을 활용한 코로나 대응 정책 만들기 - Sony AI
스탠포드 유튜브 강의(CS234)로 강화학습을 공부한 게 올해 1~2월 쯤이었다. 마냥 공부만 하면 재미가 없으니 Cartpole 예제로 직접 구현해보는 시간도 가졌더랬다(관련 글). 대학원에 입학하게 되
mech-literacy.tistory.com
'트렌드 한눈에 보기 > 학계 트렌드' 카테고리의 다른 글
| 탐조 입문자를 위한 딥러닝 활용기 - 3편 (0) | 2021.02.14 |
|---|---|
| 탐조 입문자를 위한 딥러닝 활용기 - 2편 (0) | 2021.02.09 |
| PyTorch를 활용한 Soft Actor Critic - 1탄 (0) | 2021.02.04 |
| PyTorch를 활용한 Actor-Critic Tutorial 3탄 (0) | 2021.02.03 |
| PyTorch를 활용한 Actor-Critic Tutorial 2탄 (0) | 2021.02.01 |



