
Lecture 2: Markov Decision Process가 주어졌을 때 올바른 결정을 내리는 방법
Markov Decision Process(MDP)란 무엇인지, 올바르단 것은 무엇인지 확인하면 됨
MDP 이외에도 Markov Reward Process 같은 게 등장하는데 핵심은 역시 MDP라는 것을 잊지 말자

Markov Process:
지난 시간에도 나왔지만, 핵심적인 내용이므로 다시 보면 좋음
과거의 정보가 현재 상태에 모두 녹아있어서, 미래는 현재 상태만 관찰해서도 알 수 있음
즉, 미래는 과거와는 상관이 없다, 현재 상태만 있다면.

Markov Process의 구성
Markov Process는 1. 한정된 수량의(무한대도 상관없다) 상태(State) 값과, 2. 한 상태에서 다른 상태로 너어갈 수 있는 확률로 표현될 수 있다. 알아보기 쉽게 매트릭스 형태로도 표현 가능하며 컴퓨터는 이 매트릭스 형태로 Markov Process를 이해한다.
교수님은 주식 시장에도 적용할 수 있다고 하는데, 실제로 과거의 모든 정보가 현재 주가에 반영되어 있을테니 강화학습으로 주가를 예측할 수 있을까-? 하는 호기심이 솟는다.
어쨌든 현재 Markov Process에는 "reward"나 "action" 변수가 포함되어 있지 않다. 그냥 상태 값과 확률로만 존재한다. MDP까지 뭐가 더 추가되어야 하는지 차차 보여줄 것이다.

Mars Rover로 예시를 들면 위와 같다. 예시가 친절하게 등장하는 것은 강의 몇 화에 한정되어 있으므로 지금 이 순간에 감사하도록 하자.
Markov Reward Process
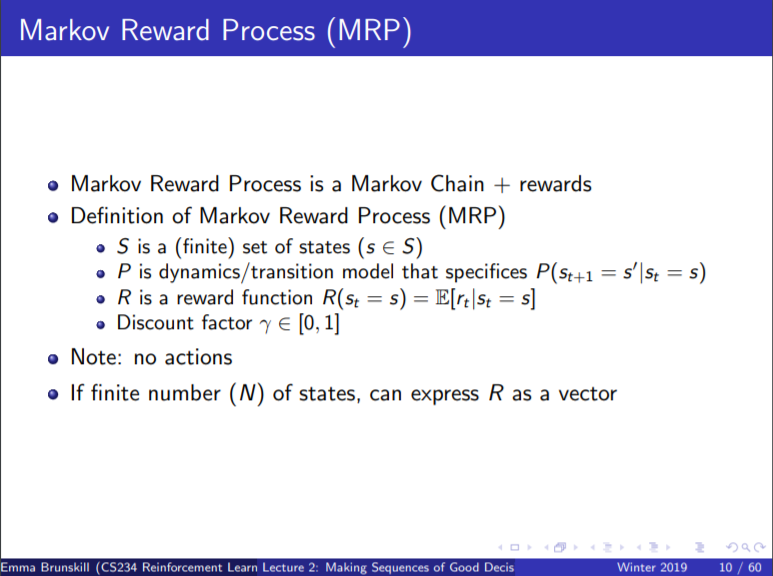
Markov Process에 보상을 추가해준 모델. 아직 "action"까지는 추가되지 않아서 MDP가 아니다. 그냥 앞서 나온 Markov Process에서 현재 상태에 있음으로서 어떤 보상(R)을 받는지 추가해 줬음.
현재 변수는 S, P, R 그리고 R을 더해줄 때 필요한 gamma 로, 세 개 같은 네 개.

Reward가 등장했으므로, 앞으로 받을 보상들의 현재 가치인 Value Function을 계산할 수 있다. 이 때 Discount Factor를 사용해서 미래에 받을 보상에 얼마나 집중할 것인가를 결정한다. 다시 말해, 마시멜로 이야기로 살 것인가, 아니면 김어준처럼 살 것인가. Discount Factor가 0이면 김어준, 1이면 마시멜로 이야기.

Value Function은 행렬로 복잡하게 계산할 수 있다. Reward 모델과 한 상태에서 다음 상태로 넘어가는 확률 행렬만 있다면 각 상태의 Value Function을 역행렬을 통해 간단하게 계산할 수도 있다는 뜻.
사실 말이 간단하게 역행렬이지, 역행렬을 구하는 것 자체가 상당히 복잡해서 상태 값이 많아질수록 계산량이 급격하게 많아진다. 위 슬라이드의 아래 줄에 O(N^3)이란 것이 바로 상태 값 수량의 세 제곱에 비례하도록 계산 복잡도가 올라간다는 뜻이니 정말 기똥차게 복잡한 셈이다.

더 간단하게 Value Function을 구하는 방법
- dynamic programming
계산 복잡도를 조금 줄이기 위해 value function은 근사값으로 많이들 구해진다. 첫 번째 근사치 계산방법은 Dynamic Programming이라고 하여, 계산을 여러 번 반복해서 돌리면서 참 값에 가까워지는 것이다.
원리는 다음과 같다. Value function이 결국에는 지금 당장의 보상에다가 앞으로 받을 보상을 discount factor에 곱해서 더해준다는 개념이다. 그래서 처음 value function 의 값을 모든 상태에 대해 0으로 잡아준 뒤 같은 계산을 반복하는 것이다. 예를 들어 2개의 상태가 있어서 reward와 P 행렬이 다음과 같이 주어졌다고 가정하자.

그럼 value function은 다음과 같이 구해지는 것이다.

Matlab으로 표현하면 아래와 같다.
R = [1 10]';
P = [0.6 0.4; 0.3 0.7];
gamma = 0.3;
v = zeros(2,9);
for i = 2:10
v(:,i) = R + gamma*P*v(:,i-1);
end
answer = inv(eye(2)-gamma*P)*R;
------------------------------------
answer =
3.1240
13.0141
10번의 반복 계산으로 상당히 참값에 가까워졌다. 2x2 행렬의 경우 단순히 역행렬을 구하는 게 더 빠르겠지만, 행렬의 차원이 커질수록 시간이 오래걸릴 것이다.
- 앞에서 상태값이 무한대여도 상관없다고 했는데, 이 경우에는 행렬로 나타내기가 어려울 것이다. 해당 경우도 추후에 다룰 것이니 걱정말고 공부할 것!
- 또한 역행렬이 존재하지 않는 경우에 대해서 우려할 수 있지만, P가 확률 행렬이기에 discount factor가 1이 아닌 한 I - discount factor * P 의 역행렬은 반드시 존재한다고 한다. 자세한 이유는 설명이 길어지므로 생략!

Markov Decision Process
Markov Reward Process에 행동(action) 변수까지 추가하면, 드디어 Markov Decision Process가 된다. 최소한의 단위로 말하자면 (S,A,P,R, discount factor)가 되는 셈이다.

이 슬라이드가 조금 헷갈리는데, 조금 위에서는 분명히 MRP에 action을 추가하게 되면 MDP라고 해 놓고서 이제 와서 MDP에 policy를 추가하면 MRP라고 하고 있기 때문이다.
MRP는 네 개의 값 (S, R, P, gamma) 로 이뤄지고 MDP는 다섯 개의 값 (S,A, P, R, gamma)로 이뤄진다. Policy는 해당 상태에서 어떤 행동을 취할 것인지 선택하는 기반이 되므로, R과 P에 A가 녹아들어가면서 MDP + Policy = MRP가 된다는 요지로 생각된다. 좀 더 쉬운 설명은 없었을까?
어쨌든 이렇게 함으로써 MRP에서 value function을 구한 것과 같은 방식으로, MDP에서는 행동지침(policy)의 value function 을 구할 수 있다는 결론을 내릴 수 있다.

예제를 풀어보자.
Discount factor가 0일 때, 무조건 왼쪽으로만 보내는 행동지침의 value function은 어떻게 되는가?
Value function 공식 우변의 우항이 모두 0이 되므로, value function은 상태에 대한 즉각적인 보상만을 다루게 된다. 그래서 [1 0 0 0 0 0 10] 이라는 값을 가지게 된다.
행동에 대한 보상을 value로 가질 때는 [1 1 0 0 0 0 10] 이 맞겠지만, Mars rover 예제를 들고나온 때부터 state에 대한 보상을 주기로 했으므로 [1 0 0 0 0 0 10] 으로 하는게 적합하다.
그런데 역시 조금 헷갈린다. 행동 지침의 value를 판단하는 문제이니, 어떤 상태에서 어떤 행동을 했을 대의 보상이 얼마인지에 초점을 둬야하는 것 아닌가? 흠...

그럼 이 경우에는 계산이 어떻게 될까? $V^p_k(s_6)$의 값을 구하는 문제인데, 단순히 전체 행렬을 곱해서 구하는게 아니라 P의 부분적인 값만 주어졌을 때 해당하는 식을 잘 세울 수 있어야 한다.

뭐 이런 식으로 복잡하게 식을 세워서 구할 수도 있겠지만, 다시 생각해보면 $s_6$에서 $s_7$으로 가야 10의 보상을 받고 현재는 보상이 0이므로 10*0.5*0.5 를 해서 2.5 가 나올 것 같다. 물론 바로 다음 단계의 value를 구한 것이므로 무한 등비수열의 합으로 구하지 않은 것이지 전체 value를 구하자면 2.5 + 0.5*2.5 + 0.5*0.5*2.5 ... 하는 식으로 구해야 할 것이다.

MDP Control
자 이제 MDP의 목적이라고 할 수 있는, 최적의 행동지침을 구할 차례다. 상태값과 행동 경우의 수에 따라서, 선택할 수 있는 행동지침은 $S^a$ 개가 된다. 7개의 상태에 2가지 행동 방식이 있다면 128개의 행동지침이 가능한 것이다. 그 중에서 value function을 가장 높게 만드는 policy가 존재할 것이므로 그걸 찾아내면 된다.
단순한 방법으로는 행동지침의 value를 몽땅 계산하는 것이 있겠지만 역시 더 나은 방법이 있다. 바로 Policy Iteration이다.

MDP Policy Iteration
쉽게 말하자면, V가 가장 높아질 때까지 행동지침을 계속 바꿔주면서 더 이상 행동지침이 변하지 않을 때가 최적의 상태라는 것이다. 사실 너무 쉽게 말한 것이라, 하나 마나 한 말이 되어 버렸다. 행동지침을 어떤 식으로 바꿔줘야 하는가- (Policy Improvement)하는 것이 핵심이기 때문이다.

이 때 필요한 것이 State-Action Value Function인 Q이다. "강화학습"하면 유명한 영상인 벽돌깨기 알고리즘이 DQN이라고 해서, Deep Q Learning의 줄임말인데 그 Q이다. 그만큼 정말 중요한 개념인 것이다.
V와 Q의 차이점이 무엇인지 보다 자세하게 알아보자. $V^\pi(s)$는 상태 s에 있을 때 행동지침 $\pi$를 따르면 받게 될 보상의 현재 가치였다. 반면에 $Q^\pi$는 행동지침 $\pi$를 따르긴 할 건데, 지금 당장이 아니라 행동 a를 취한 다음에 행동지침에 따라 움직이겠다는 것이다. 행동 a는 행동지침 $\pi$가 시키는 것과 다를 수 있다.
잘 와닿지 않는다. 예시가 있으면 좋을 텐데 일단 policy improvement 방법을 살펴본 다음에 확인하도록 하자.

Policy Improvement
행동지침 평가(Policy Evaluation)를 통해서, value of the policy $V^\pi$를 구한 다음에 어떻게 더 나은 행동지침을 만들어 낼 수 있는지에 대한 방법이다. 이 방법은 P행렬 (상태가 변할 확률 행렬, dynamics model) 과 보상에 대한 완벽한 정의가 있어야 가능하다. 하지만 이들이 모두 정의되는 경우는 실생활에서 많이 찾아볼 수 없으므로 다른 방법을 써야하는데 이는 나중 강의에서 나온다. 일단은 이상적인 케이스에 대해 논의해보도록 하자.
첫 번째로 해당 행동지침에 대한 Q 값을 구하는 것이다. Q는 앞서 말했듯, 현재 행동지침과는 다를 수 있는 행동 a를 취한 다음에 그 행동지침을 따를 경우에 받는 보상의 현재가치이다. 두 번째로는 그 Q값을 최대화 시켜주는 a값을 찾아서 그 다음 행동 지침으로 삼아주는 것이다.
말로 쓰니 더 아리송하다. 처음 이 글을 접했더라면 침뱉고 갔을 것이다. 얼른 예시가 나왔으면 좋겠다만, 강의를 끝까지 넘겨보니 예시는 등장하지 않는다. 퉤퉤퉤.
별 수 없이 이 부분에 대한 확실한 이해는 나중을 기약해야겠다.

Policy Improvement에 대한 개념적인 설명
핵심 원리를 수학적으로 이해하지 못하겠으니, 개념적으로 먼저 이해하고 넘어가도록 하자. policy improvement의 원리는 수 없이 많은 선택의 연속으로 이뤄진 행동지침에서, 어떤 행동의 변화가 전체 행동지침의 가치를 높여준다면 그 선택을 밀고 나가야 한다는 것이다.
친환경 의류 생산 회사에서 일하는 당신이, 공연 기획사로 이직할 수 있는 기로에 서 있다고 가정하자. 그리고 모든 요소를 고려한 결과 이직을 해서 현재 삶이 나아졌지만, 가끔씩 "여전히 그 회사에 있었으면 어땠을까?" 하는 고민을 하곤 한다. policy improvement는 그런 고민이 전혀 쓸 데 없다는 것을 말한다. 분명히 현재 상태보다 좋지 않았을 것이니 헛소리 하지 말고 어서 다음 행동이나 고민하라고 재촉한다.
이렇게 확신을 가질 수 있는 이유는 강화학습이 Markov Process에서 이뤄지기 때문이라고 생각된다. 어쨌거나 현재 상태는 과거의 모든 정보를 담고 있기에, 현재 상태에서 내린 결론은 어떻게 봐도 최선의 선택인 것이다. "계속 친환경 회사를 다녔다녀 갑자기 해외출장이나 승진의 기회가 찾아오지는 않았을까?"하는 공상은 백일몽에 지나지 않는다. 바이든이 미국 대선에서 이기면서 친환경 산업 붐 열풍이 불어 "아 그냥 계속 다닐걸" 하는 후회를 하는 것은 모든 정보를 담지 못한 탓이다.

Value Iteration
한편, Policy Iteration 이외에 최적의 행동지침을 구하는 다른 방법이 있다. Value Iteration이 구체적으로 Policy Iteration과 어떻게 다른지는 강의 설명이 잘 와닿지 않아 stackoverflow를 찾아보았다.

위 알고리즘은 관상용으로 넣어둔 것이고, 둘의 차이점은 아래와 같다.
- Policy Iteration = policy evaluation + policy improvement. 우 변의 항들은 모두 행동지침이 수렴할 때까지 반복된다.
- Value Iteration = finding optimal value function + one policy extraction
하지만 이보다 핵심은 두 알고리즘이 상당히 유사하다는 것, 그리고 최적의 행동지침을 찾는데는 policy iteration이 더 빠르게 작동한다는 점이다. Value Iteration은 잊어버려도 상관없다.
그러므로 강의 마지막에 나오는 Bellman Operation에 대한 이야기는 무시해도 좋다.
'트렌드 한눈에 보기 > 학계 트렌드' 카테고리의 다른 글
| [CS234] Lecture 4: Model Free Control 정리 (0) | 2020.12.12 |
|---|---|
| [CS234] Lecture 3 - Model Free Policy Evaluation 정리 (0) | 2020.12.11 |
| [CS234] Reinforcement Learning: Lecture 1 정리 (0) | 2020.12.09 |
| [서울대 기계과] 웨어러블의 방향은 아이언맨을 향해 가고 있나요? (하편) (0) | 2020.12.08 |
| [서울대 기계과] 웨어러블의 방향은 아이언맨을 향해 가고 있나요? (상편) (0) | 2020.12.07 |



