1편에서 이어집니다.
예제와 함께 단숨에 이해하는 Lyapunov Stability [1/2]
0. 배경 "단숨에"라는 부사와 [1/2]라는 편명이 조화롭지 않다는 것은 알고 있다. 하지만, Lyapunov를 단숨에 이해하기는 불가능하다. 혹시 너무 직관적으로 이해하고 있다면, 제대로 이해하지 못했
mech-literacy.tistory.com
1편을 쓴 지 17일이 지났는데, 이제서야 2편을 쓰는 이유는 오늘에서야 Lyapunov를 이해했기 때문이다. 이해라기 보다는 계산 방법을 깨달았다는 수준에 그치겠지만, 여튼 내가 사용할 수 있기까지 2주가 넘는 시간이 걸렸다. 이게 뭐라고... 싶지만, 막상 알고보니 이거 참 유용하다. 예제를 활용한 Lyapunov stability 계산법, 정확히는 Maximum Lyapunov Exponent 계산 방법을 정리해봤다.
0. 데이터 수집
본 예제에서 사용하는 데이터는 인간 보행 중 다리 사이 각도를 활용했다. 20Hz로 대략 4분 이상 걸은 결과물인데, 정확히 몇 분 이상부터 stability를 계산 가능한지는 아직 모르겠다. 실제 활용하기 위해서는 어느 정도데이터가 필요한지가 제일 중요하기 때문에 시일 내에 확인해봐야할 일이다.
1. Phase State Reconstruction
1편에서 간단히 설명했지만, phase state reconstruction의 목적을 한 줄로 설명하면 아래와 같다.
set of all possible states that the system can evolve into
오히려 더 무슨 말인지 모르겠지? ChatGPT가 써준 말이다. 말이 멋있어서 갖고왔다. 약간 평행우주로 나아가는 느낌... 사진으로 설명하면 아래와 같다.


그림 1의 original data는 phase state reconstruction을 통해, 그림 2처럼 3차원으로 그려졌다. 이 때, embedding dimension, time delay라는 두 개의 parameter를 통해 reconstruction이 이뤄진다. Original data의 형태가 [500 x 1], embedding dimension = 3, time delay = 5라면, reconstructed data의 형태는 [500 - (3 - 1) * 5, 3] 이 된다.
Embedding dimension과 Time delay를 구하는 방법은 참고문헌 [1], [2]을 보면 된다. 상당히 다양한데, 다 알기에는 막막하니 대부분의 경우에서 Embedding dimension은 5 이상, Time Delay는 주기의 10% 정도를 사용하는 것으로 알면 된다. 사실 참고문헌 [2]에서도 Time Delay를 주기의 3%~17% 로 사용한다고 하니 그렇게 중요한 파라미터도 아닐 수 있다. 다만, embedding dimension의 경우 3차원까지만 그림으로 표현할 수 있으므로 예제에서 그려지는 그림들은 3을 사용했다.
2. Nearest Neighbor Selection

Nearest Neighbor는 phase state reconstruction을 통해 그려낸 궤도 상에서 reference point에 가장 가까운 점들이다. 본래는 가장 가까운 하나만 사용해서 계산했지만, 이후에는 5개 이상, 더 잘 계산하려면 15개까지는 써야 한다는 것이 밝혀졌다 [3]. 하지만 어디까지나 데이터 유형에 따라 취사 선택해도 무방하다.
3. Distance Calculation
이제 가장 가까운 점들의 거리가 어떻게 변화해 나가는지 계산하면 된다. 이 부분이 이해가 가지 않아 2주가 걸렸더랬다. MATLAB 코드는 아래와 같다.
% Y3: phase state
% indices: nearest neighbor's index
% length(distance) == length(Y3) - eRange;
eRange = 200;
steps = (1:eRange)';
for i = 1:length(steps)
shift = steps(i)-1;
di = sum((Y3((1:length(distance)) + shift, :) - Y3(indices + shift, :)).^2, 2);
dist(i) = mean(log(di))*20;
end
사진을 보면 이해가 간다. 사실 안갈 수도 있다. 여튼 timestep 1을 보면, reference point와 그 이웃점들이 그려져있다. timestep 2에도 동일하게 그려져있는데, 서로 거리가 살짝 멀어진 것을 볼 수 있다. 이런 식으로 계산하는 것이다. 쉬우면서도, 3차원 데이터를, 또는 그 이상 차원의 데이터를 머릿속에 그리는 것이 쉽지 않을 수 있다. 난 2주가 넘게 걸렸다. MATLAB에서는 lyapunovexponent라는 함수를 통해 자동으로 계산해준다.
4. 결과
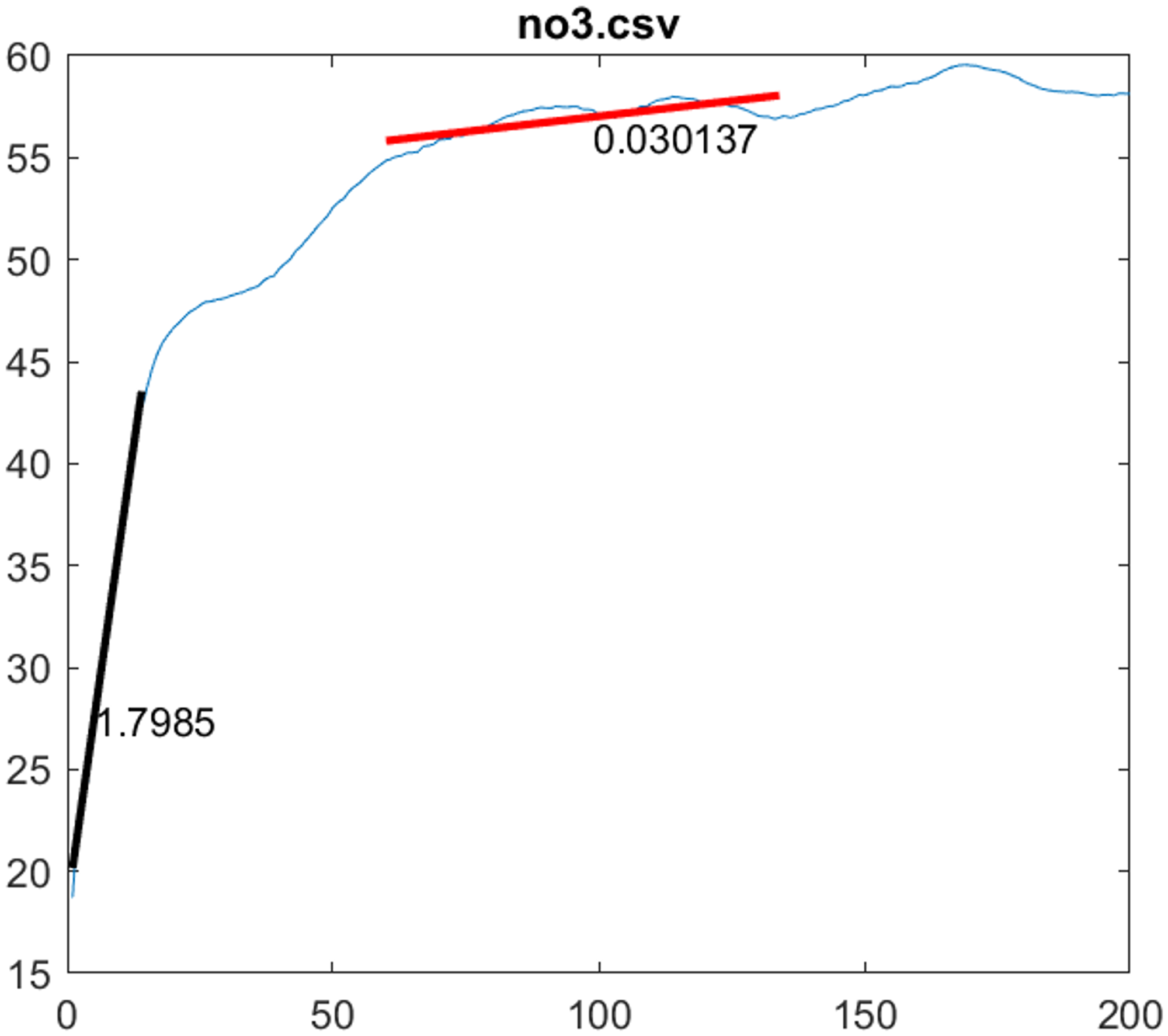
이렇게 계산한 결과는 상당히 쓸만 했다. 잘 못 걷는 사람은 값이 크게, 잘 걷는 사람은 값이 작게 나오고, 운동 회차가 진행될수록 값이 작아진다. 앞서 말했듯이, 어느 정도 데이터 - 몇분 이상 걸었을 때부터 stability를 계산할 수 있는지, 실시간으로 계산 가능한 수치인지는 확인해봐야겠지만, 그동안 쓰던 평가지표들보다 훨씬 안정적이다. 익히는데 시간이 좀 걸렸지만, 앞으로 좀 더 자유롭게 사용해보기를 기대해본다.
참고문헌
[1] Rosenstein et al., “A practical method for calculating largest Lyapunov exponents from small data sets”, 1993
[2] Granata et al., “The influence of gait speed on local dynamic stability of walking”, 2007
[3] Mehdizadeh, “A robust method to estimate the largest Lyapunov exponent of noisy signals: A revision to the Rosenstein’s algorithm”, 2019
'트렌드 한눈에 보기 > 학계 트렌드' 카테고리의 다른 글
| Diffusion Model을 이해해보자 2편 - chatGPT로 튜토리얼 생성 망한 이유 (0) | 2024.05.16 |
|---|---|
| Diffusion Model을 이해해보자 1편 - 태초마을 (0) | 2024.05.12 |
| 예제와 함께 단숨에 이해하는 Lyapunov Stability [1/2] (2) | 2024.01.13 |
| [Bayesian 1차] 모르면 모른다 말하는 Deep Learning - "What Uncertainties Do We Need in Bayesian Deep Learning for Computer Vision?" (1) | 2023.12.28 |
| [2023 ver.] tensorflow에서 GPU를 사용하는 방법 Windows (1) | 2023.11.29 |



