
Lecture 6에서는 지난 시간에 배웠던 VFA(Value Function Approximation)을
Deep Neural Network (특히 CNN)을 통해 구현하는 방법을 배울 것이다.

이상적인 모델은 Oracle이라는 존재로부터 Value Function에 대한 참값을 받은 후
근사값과의 오차를 계산해서 그 오차를 줄여가는 방법으로
학습에 필요한 V 와 Q 값을 계산하는 것이었지만, Oracle은 존재하지 않는다.
그래서 몬테카를로나 TD Learning을 이용한 값을 Value Function 참값 대신에 집어넣는 것이었다.
하지만 DNN이 발달하면서 Linear VFA보다 더 잘 작동하게끔 참값을 추정할 수 있음이 밝혀졌고,
강화학습 분야에도 사용이 확산되었다.
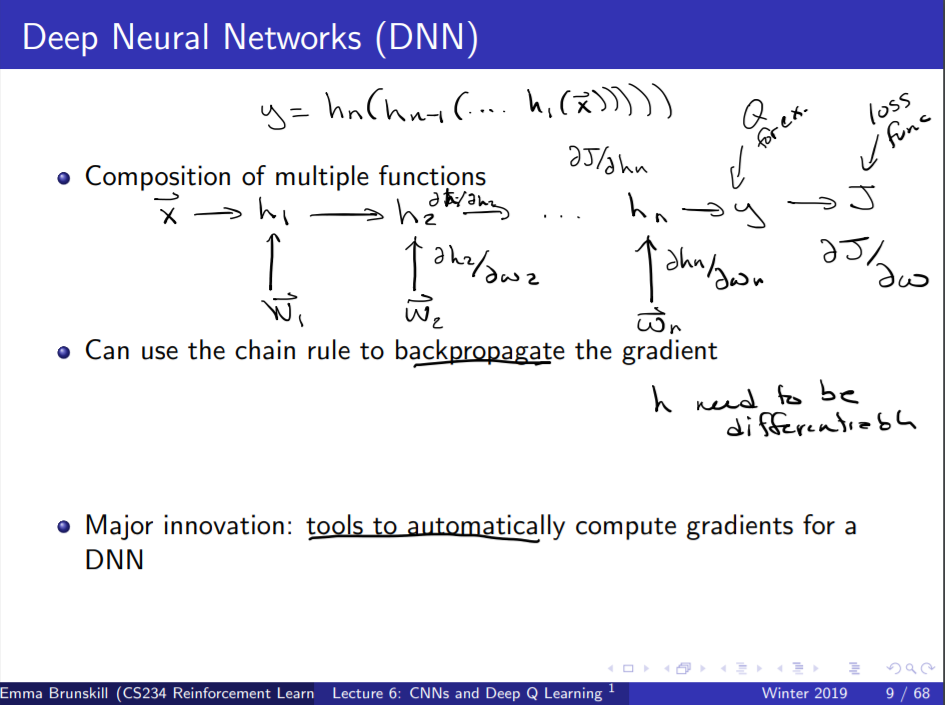
DNN은 위 슬라이드에 보이는 도식으로 설명가능한데,
input X에 여러 겹의 파라미터가 붙으면서 최종적으로 output y를 내뱉는 방식이다.
여기서 input x를 구성하는 방식으로서 CNN이 많이 쓰이고
파라미터를 붙이는 방식 또한 다양하게 연구되어 각각 과목이 한 가지씩 생겼을 정도이다.
강의에서도 간략하게 해당 내용을 설명해주지만, 수박 겉핥기에 지나지 않는다.
CS231n을 한번 듣거나, 여러 Medium등의 포스트를 참고하면서
인사이트를 키워놓는 것이 좋을 것 같다.

그래서 Deep Learning과 Q Learning을 활용해서 Atari를 어떻게 플레이했느냐,
게임 이미지 네 장을 입력변수로 넣고, CNN을 통해 Q를 학습한 뒤
강화학습 알고리즘을 돌렸다는 것이다.
아타리 게임이 상당히 다양한데, 몇 개는 들어봤지만(대표적으로 벽돌깨기)
대부분은 처음 들어보는 것들이다(몬테주마, 퐁 등).
해당 게임들을 학습시키는 데 동일한 구조를 사용했음에도
준수한 성적으로 학습을 완료했다고 한다.
하지만 사실은 그렇게 준수하지만은 않다.

일반인이 플레이하는 실력을 70%로 봤을 때(전문가가 100%),
전체 아타리 게임의 60% 정도만 그 이상의 점수를 획득할 수 있었던 것이다.
낮은 비율은 아니지만 그렇게 높다고할 수도 없는 비율이다.
여전히 강화학습에 발전이 필요한 영역이 많이 있음을 보여준다.

어쨌든, DQN에서는 게임을 플레이하기 위해 다양한 방식으로 알고리즘을 수정했는데
대표적인 문제는 샘플들이 서로 연관되어 있다는 것이다.
$(s, a, r, s', a', r', s'')$로 이루어진 tuple에서 s와 s'이 연관되어 있지 않을 수가 없다.
예를 들어 자동차 자율주행을 강화학습을 통해 수행하고 있을 때
차가 언덕길을 오르는 구간에서 학습을 시키게 된다면
자연스레 엑셀을 더 밟는 쪽으로 파라미터가 형성되면서
평지에서도 가속하는 모습을 보게 될 것읻.ㅏ
두 번째 문제는 Non-stationary Target이라는 것이다.
이게 무슨 뜻인지 도통 이해할 수가 없었는데, VFA의 방식을 보면 조금이나마 감이 온다.
Q function( = state action value function)을 학습시키기 위해서는
$Q = R(s, a) + \gamma * max_a Q(s', a')$를 반복계산해야 하는데
Q 자체가 계속 업데이트 되다 보니, $max_a Q$를 계산하는 데도 시간이 오래 걸리는 것이다.

DQN은 Sample correlation을 해결하기 위해서 Experience Replay를 도입했다.
TD Leanring에서 한 에피소드를 (S, A, R, S')로 구성되는 여러 개의 tuple로 나눴듯이
Replay Buffer라고 불리는 데이터셋을 구성해서 과거 경험들을 저장해두는 것이다.
그럼으로써 데이터 메모리가 좀 쓰이겠지만,
우선 데이터를 한 번 쓰고 버리는 것보다(TD Learning에서 처럼) 더 효율적으로 활용할 수 있다.
또한 Q function 학습 과정에서 샘플을 얻은 순서대로 제공하는 것보다
데이터셋에서 무작위로 추출해서 제공하게 된다면 데이터 연관성도 줄여줄 수 있다.

Non-stationary target을 해결하기 위해서는
Q값을 학습시키는데 필요한 파라미터를 고정시키는 방법을 사용했다.
물론 학습 내내 고정시킨다는 뜻은 아니고(학습이 이뤄지지 않을테니)
몇 번의 반복과정에서 고정한 뒤, 살짝 업데이트해서 다시 고정하는 방식으로 사용했다.
위 슬라이드에서 $\Delta w$ 식을 보면, $max_a Q$ 부분에 $w^-$로 표기된 것을 볼 수 있는데
그 부분이 바로 한시적으로 고정되어 있는 파라미터이다.

DNN, Replay Buffer, Fixed Q를 활용하는 것이
성능에 얼마나 큰 영향을 미치는지(숫자가 클수록 좋다) 알아본 표인데
Replay Buffer가 성능 향상에 가장 큰 영향을 끼쳤다는 것을 볼 수 있다.
단순히 데이터 샘플 간의 연관성을 줄여주는 것 이외에도 성능이 있는 것인지
확인해 볼 필요가 있어 보인다.
강의 중 질문으로서는, 왼쪽 두 열만 보았을 때
Linear VFA가 DNN VFA보다 더 잘 작동하는 것처럼 보이기에
Linear VFA와 Replay Buffer, Fixed Q를 섞으면 어떻게 되는지 확인해볼 필요가 있다.
교수님의 설명은 역시 어물쩡 넘어가버렸고, 명확한 답이 제시되지 않았다.

DQN이 2015년에 발표되었고, 1년 후에 그 응용버전들이 많이 생겨났다.
대표적인 사례가 몇 가지 있는데, 첫 번째는 Double DQN이다.
지난 번 강좌에서 배운 Double Q Learning에 DNN을 활용한 것인데,
그 때도 간단히 짚고 넘어갔었고 이번에도 간단히 짚고 넘어간다.

하지만 성능은 그렇게 간단히 짚고 넘어갈 게 못된다.
DQN(빨간 색)이 못하는 분야를 획기적으로 잘하게 되지는 않았지만
전반적으로 효율을 확 높여주는 알고리즘인 것 같다.

두 번째 예시는 Priortized Replay이다.
Replay buffer에서 어떤 값을 사용해서 학습을 시키느냐가
VFA에도 큰 영향을 끼치게 된다.
TD Learning에서 배웠던 대로, 하나의 에피소드를 4가지 tuple로 나눈 뒤
순차적으로 학습한다면 [1 0 0 0 0 0 0 0]이라는 VFA를 얻게 되지만
3번 tuple, 1번 tuple을 먼저 학습시킨다면 [1 1 1 0 0 0 0]을 얻게 된다.

Replay Buffer에서 우선순위를 둬서 추출하는 방식은
학습 시간을 기하급수적으로 줄여줄 수 있다고 한다.
하지만, 어떻게 우선순위를 둘 지 결정하는 게 어려워 보이는데
위 슬라이드와 같은 방식을 사용한다.
쉽게 말하면 TD 오차가 큰 tuple을 먼저 수행함으로써
오차를 더 빠르게 줄여준다는 것이다.
자세하게 설명하지는 않았으나, 이 정도면 나중에 필요할 때 써먹을 수는 있겠다.
이외에도 Dueling DQN 이라는 방법이 있지만,
원체 빠르게 지나가서 이해하기 힘들었다.
DQN은 계속 발전했으니, 강의 후 2년이 지난 지금은 더 발전했을 테다.
나중에 정말 필요하다면 Dueling DQN보다 더 좋은 알고리즘을 공부해야 할테니
그 때 가서 생각하기로 했다.
'트렌드 한눈에 보기 > 학계 트렌드' 카테고리의 다른 글
| [CS234] Lecture 8: Policy Gradient I 정리 (0) | 2020.12.18 |
|---|---|
| [CS234] Lecture 7: Imitation Learning 정리 (1) | 2020.12.17 |
| [CS234] Lecture 5: Value Function Approximation 정리 (0) | 2020.12.15 |
| [CS234] Assignment 1 풀이 (0) | 2020.12.14 |
| [CS234] Lecture 4: Model Free Control 정리 (0) | 2020.12.12 |



